포아송분포(Poisson distribution) 2009/08/29 11:59
|
다음 급수를 살펴보자. 이 급수는 모든 m값에 대하여 em으로 수렴한다. 그렇다면, 다음과 같이 정의되는 함수 p(x)를 고려해보자. m > 0 이므로, p(x) ≥ 0 이며 다음이 성립한다. 따라서, p(x)는 이산형 확률변수의 pmf가 될 조건을 만족한다. p(x)와 같은 pmf를 가지는 확률변수는 모수가 m인 포아송분포(Poisson distribution)를 따른다고 하며 p(x)를 모수가 m인 포아송확률질량함수(Poisson pmf)라고 한다. 일반적으로 단위시간이나 단위공간에서 어떤 사건의 출현횟수가 갖는 분포를 포아송분포라고 한다. 예를들어 어느 전화안내에 5분동안 걸려오는 전화번호 문의 횟수라든가 어느 특정지역에서 하루동안 발생하는 교통사고 건수 등을 나타내는 확률분포이다. 만약 어떠한 과정(process)이 포아송분포를 따르게 되면, 그 과정을 포아송과정(Poisson process)이라 부른다. g(x, w)를 각각 w만큼의 구간에서 일어난 사건 x들의 확률이라고 정의하자. 그리고 기호 o(h)를 다음과 같은 함수 를 표현한다고 하자. 포아송 가정은 다음과 같다. 1. 2. 3. 겹쳐지지 않는 구간들에서 일어난 사건의 수는 독립이다. 가정 1과 3은 짧은 구간 h에서 일어난 한 사건의 확률은 겹쳐지지 않는 다른 구간에서 일어난 사건들과 독립임을 나타내고 그 확률은 대략 구간의 길이에 비례함을 나타낸다. 가정 2의 요지는 동일한 짧은 구간 h에서 발생한 둘 이상의 사건의 확률은 본질적으로 0과 동일하다는 것이다. 만약 x=0이면, g(0, 0)=1이다. [출처] 포아송분포(Poisson distribution)|작성자 ColDragon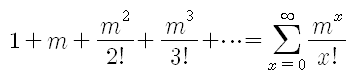
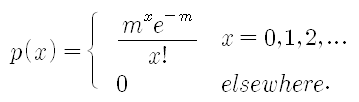 (단, m>0)
(단, m>0)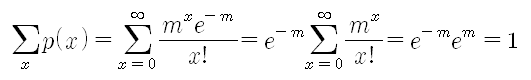
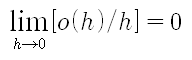 예를들어, h2 = o(h), o(h) + o(h) = o(h)
예를들어, h2 = o(h), o(h) + o(h) = o(h)![]() , λ는 양의 상수이며 h > 0
, λ는 양의 상수이며 h > 0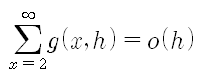
'Professionality' 카테고리의 다른 글
| IT 업계를 바꿀 차세대 프로그래밍 언어 톱10 (0) | 2012.01.06 |
|---|---|
| NIH 신드롬 (0) | 2011.01.13 |
| 사라지는 도시 (0) | 2010.11.22 |
| What is Biomedical Engineering? (0) | 2010.11.04 |
| [TED] 소비자의 요구 알아내기 (0) | 2010.08.25 |